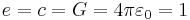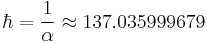Stoney units
In physics the Stoney units form a system of units named after the Irish physicist George Johnstone Stoney, who first proposed them in 1881. They are the first historical example of natural units, i.e. units of measurement designed so that certain fundamental physical constants serve as base units. The set of constants that Stoney used as base units is the following [1][2]:
- Elementary charge, e;
- Speed of light in a vacuum, c;
- Gravitational constant, G;
- Coulomb constant, 1/(4πε0).
This means the numerical values, in terms of Stoney units, of all these constants equal one:
Stoney's set of base units is similar to the one used in Planck units, proposed independently by Planck thirty years later, but Planck replaced the elementary charge with the Planck constant.[3] In Stoney units, the numerical value of Planck's constant is not 1, but is
where α is the fine-structure constant. Planck units are more commonly used than Stoney units in modern physics, especially quantum gravity (including string theory). Rarely, Planck units are referred to as Planck-Stoney units.[3]
Contents |
History
George Stoney was one of the first scientists to understand that electric charge was quantized; from this quantization he deduced the units that are now named after him.[4] [5] James G. O’Hara[6] pointed out in 1974 that Stoney’s derived estimate of the unit of charge, 10−20 ampere-second, was 1⁄16 of the modern value of the charge of the electron. The reason is that Stoney used the approximated value of 1018 for the number of molecules presented in one cubic millimetre of gas at standard temperature and pressure. Using the modern values for Avogadro’s number 6.0238×1023 and for the volume of a gram-molecule (at s.t.p.) of 22.4146×106 mm3, the modern value is 2.687×1016, instead of Stoney's 1018.
Stoney units and Planck units
The Stoney length and the Stoney energy, collectively called the Stoney scale, are not far from the Planck length and the Planck energy, the Planck scale. The Stoney scale and the Planck scale are the length and energy scales at which quantum processes and gravity occur together. At these scales, a unified theory of physics is thus required. The only notable attempt to construct such a theory from the Stoney scale was that of H. Weyl, who associated a gravitational unit of charge with the Stoney length[7][8][9] and who appears to have inspired Dirac’s fascination with the large number hypothesis[10]. Since then, the Stoney scale has been largely neglected in the development of modern physics, although it is occasionally discussed to this day.[11][12] The Planck scale is valid for all known interactions, and does not give prominence to the electromagnetic interaction, as the Stoney scale does.
See also
Footnotes
- ^ The anthropic cosmological principle, by Barrow and Tipler, p291
- ^ Astrophysics, clocks and fundamental constants, by Karshenboim and Peik, p79
- ^ a b Space: in science, art and society, by Penz, Radick, Howell, p191
- ^ Stoney G. On The Physical Units of Nature, Phil.Mag. 11, 381–391, 1881
- ^ G. Johnstone Stoney, On The Physical Units of Nature, The Scientific Proceedings of the Royal Dublin Society, 3, 51–60, 1883. Retrieved 2010-11-28.
- ^ J.G. O’Hara (1993). George Johnstone Stoney and the Conceptual Discovery of the Electron, Occasional Papers in Science and Technology, Royal Dublin Society 8, 5–28.
- ^ K. Tomilin, “Natural System of Units”, Proc. of the XX11 International Workshop on High Energy Physics and Field theory, (2 000) 289.
- ^ H. Weyl, “Gravitation und Elekrizitaet”, Koniglich Preussische Akademie der Wissenschaften (1918) 465–78
- ^ H. Weyl, “Eine Neue Erweiterung der Relativitaetstheorie”, Annalen der Physik 59 (1919) 101–3.
- ^ G. Gorelik, “Herman Weyl and Large Numbers in Relativistic Cosmology”, Einstein Studies in Russia, (ed. Y. Balashov and V. Vizgin), Birkhaeuser. (2002).
- ^ M. Castans and J. Belinchon(1998). “Enlargement of Planck’s System of Absolute Units”, preprint: physics/9811018
- ^ Ross McPherson. Stoney Scale and Large Number Coincidences. Apeiron, Vol. 14, No. 3, July 2007
External links
|
||||||||||||||||||||